Nunca habría pensado que las matemáticas y la Arqueología fueran a estar relacionados cuando las estudiaba en el Instituto. Siempre me han gustado las mates. Bien es cierto que mi gusto por esta materia ha sido siempre mucho mayor que mi talento en ella. No es que se me dieran mal pero tampoco era un estudiante brillante.
Lo que quiero decir con esto es que, pese a que mi camino académico ha estado marcado por las (llamadas) letras, nunca he repudiado la faceta científica y he tratado de estar siempre enganchado a asignaturas como matemáticas, física o naturales. De hecho, la Arqueología es cada vez más una disciplina interdisciplinar, y esto conlleva saber o conocer de otras materias. Y de ahí mi inquietud por alguna de estas disciplinas que ahora trato de alimentar con libros o programas de televisión de esta temática.
–
La magia de los números, el lenguaje universal
El archiconocido físico Stephen Hawkins siempre dice que si estableciéramos contacto con una civilización inteligente extraterrestre, las matemáticas, los números, sería el lenguaje vehicular para establecer la comunicación.
De hecho, la sonda Voyager contiene un disco de oro que elaboró Carl Sagan, con imágenes y fórmulas matemáticas donde se explica, digamos, la naturaleza de la tierra y se representa al ser humano, hombre y mujer, además de la localización de la Tierra en la vía láctea. Un mensaje en una botella en el inmenso océano universal con la esperanza de que alguna civilización lo encuentre y sepa leerlo.
Marcus du Sautoy es un matemático de la Universidad de Oxford cuyo principal objeto de estudio son los números primos. Además de a esto, se dedica a la divulgación de la materia. Y lo hace fantástico, dicho sea de paso.
¿Hacer las matemáticas atractivas a la gente? Pues du Sautoy lo consigue. La proporción áurea, Fibonacci, el número pi….
–

–
¿Pero de qué demonios está hablando este? ¿Se ha vuelto loco? ¿Esto no es un blog de Arqueología?
Me pitan los oídos. Sí, lo es. Pero ya sabes que no solo de Arqueología vive el arqueólogo. Y no puedo evitar comentar algunas de mis aficiones de vez en cuando. Además, quería mostrarte para qué me han servido las matemáticas en la Arqueología de campo. ¿O eres de los que estudió Historia huyendo de los números? Pues no te escaparás de ellos.
Quizás pienses que hubiera sido mejor haberme centrado en las asignaturas que me hubieran podido servir en mi carrera profesional como arqueólogo como latín o griego, que no paso del rosa, rosae o Chi Ro… Sí. Tal vez tengas razón. Debí haber prestado más entusiasmo en clase de latín o haber escogido griego en lugar de Física y Química pero, en fin, era joven (¿¡sirve como excusa?!).
–
Las cosas son números. Pitágoras
–
Sin embargo, he de decir que mi esfuerzo e inquietud por las mates no ha caído en saco roto. Y además de hacer las cuentas para llegar a final de mes, he utilizado lo que aprendí en clase de matemáticas en mi trabajo de campo.
–
 –
–
Estábamos realizando una excavación en área abierta y teníamos parte del inmenso yacimiento sobre cuadrículas. Pero me tocó seguir una Unidad Estratigráfica (UE) más allá de la cuadrícula y me encontré con un pequeño problema:
¿¡Cómo puedo recoger esta UE en un plano si no tengo la cuadrícula?!
Y mi encargado me vino a salvar la papeleta.
–
Pitágoras y la Arqueología
¿Conoces a Pitágoras?
Eso fue lo que me preguntó directamente. Pitágoras.
–Claro, Pitágoras. El griego, ¿no? ¡Ese del triángulo rectángulo!
Dejando esta simplona respuesta por mi parte, Pitágoras fue un matemático de la antigua Grecia que ha pasado a la Historia por darle nombre a un teorema matemático.
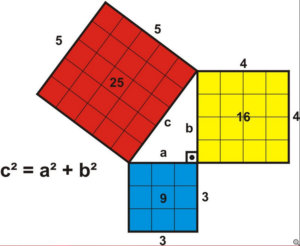 –
–Volvamos al yacimiento. Tenía cerca una sola piqueta que formaba parte de la cuadrícula del yacimiento. Y de ahí debía sacar una nueva cuadrícula o un cuadrado exacto para representar la UE en un plano. ¿Cómo?
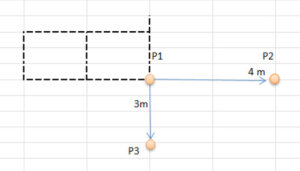
1. Coges una cuerda, o una cinta métrica mejor, y desde un cabo (punto 1) la atas a la piqueta que tienes registrada en la cuadrícula.
2. Te alejas con la cinta métrica de manera horizontal desde la piqueta (punto 1) trazando una línea recta de 4 metros (hasta el punto 2) y tratas de calibrar la línea que has formado con la cinta para que esté lo más recta posible.

3. Luego desde la piqueta de nuevo, sigues la línea hacia el lado opuesto, de manera perpendicular a la cuadrícula trazando una línea recta de 3 metros (punto 3).
4. Atendiendo al teorema de Pitágoras, tenemos dos incógnitas resueltas que es la medida de dos de los lados. 4 y 3. Entonces, c²=3²+4². Y sólo tenemos que sumar para resolver la incógnita. 16+9=25; por tanto c=5. Ya tenemos la hipotenusa.
5. Ahora sólo tenemos que unir los dos vértices de estas líneas con otra línea de 5 metros, pues es la distancia que habrá entre un lado de 3 metros y otro de 4 metros (para que sea rectángulo y tengamos la mitad de una cuadrícula).
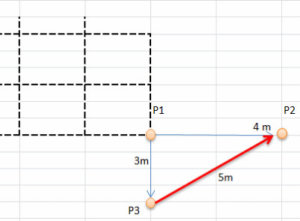
Ya tenemos un triángulo rectángulo perfecto 🙂 así que estamos en disposición de terminar el cuadrado o de pasar la UE a plano si con esos vértices tenemos suficiente.
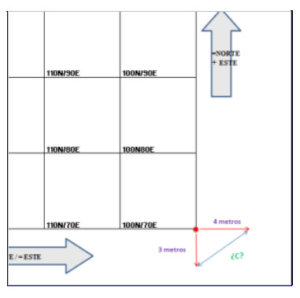
Por eso Pitágoras es inmortal. Porque más de 2000 años después de su muerte, sus elucubraciones sobre la exactitud de un triángulo rectángulo me han permitido llevar a plano una simple zanja de la edad del bronce.



